Des chercheurs du Laboratoire Jean Kuntzmann et du Laboratoire de mathématiques d'Orsay ont développé un algorithme permettant de concevoir et construire toute une famille de composants optiques, lentilles ou miroirs, permettant de transporter l'énergie lumineuse de manière optimale et précise. Leurs travaux, publiés dans la revue scientifique Transactions on Graphics, sont présentés à Tokyo lors de la conférence internationale SIGGRAPH Asia du 4 au 7 décembre 2018. Leur technique a également fait l’objet d’un dépôt de brevet*.
L’optique non imageante
L'optique non imageante, ou optique anidolique, est une branche de l'optique qui vise à concevoir des dispositifs tels que lentilles ou miroirs, réfléchissant ou réfractant la lumière émise depuis une source. Il ne s’agit donc pas de reconstituer l’image de la source mais bien d’orienter la lumière sur des trajets choisis. "
En appliquant les lois d’optique de Descartes, le défi est de calculer la forme d’une lentille ou d’un miroir de façon à concentrer la lumière exactement là où l’on veut" explique Boris Thibert, chercheur au Laboratoire Jean Kuntzmann de Grenoble.
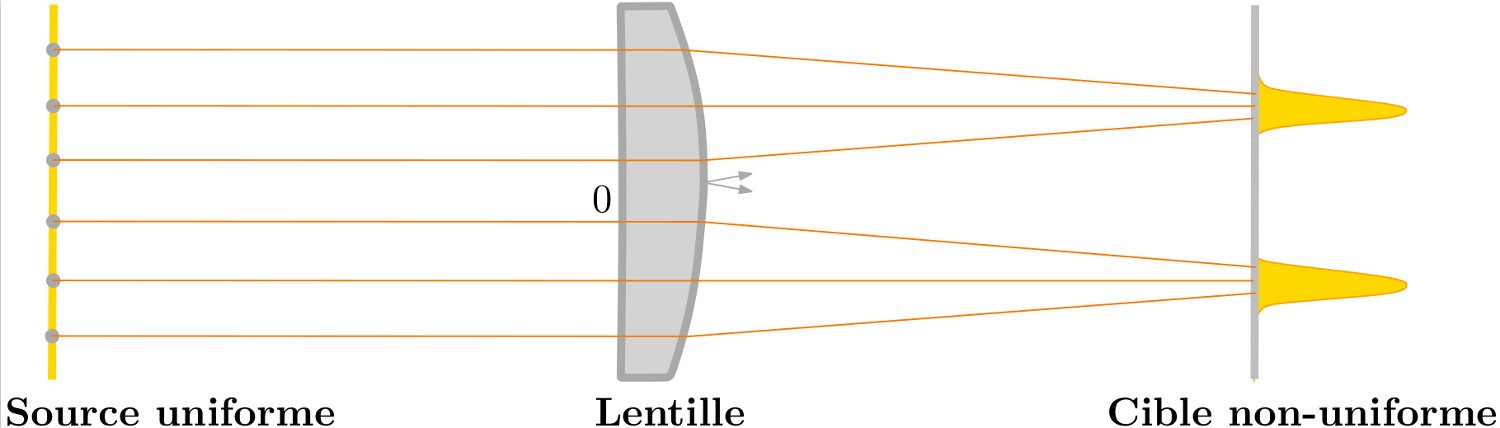
Figure 1 : Exemple de problème d'optique non imageante. La source de lumière est composée de rayons horizontaux issus d'un plan vertical. Le but est de construire la lentille qui après réfraction, va créer la distribution de lumière souhaitée en sortie. (crédit : Mérigot / Meyron / Thibert)
Les applications principales concernent la conception de fours solaires, de lampadaires, de phares de voitures, et plus généralement l'optimisation de zones d'éclairage et la réduction de la pollution lumineuse.
Optimiser le transport de la lumière : un problème mathématique
Il existe plusieurs variantes des problèmes inverses de modélisation de miroirs ou de lentilles, en fonction de la géométrie de la source lumineuse et de la cible à éclairer. L'équation principale qui régit ces problèmes d'optique non imageante est une équation de conservation d'énergie qui est une équation de type Monge-Ampère. C'est une équation aux dérivées partielles non linéaire, beaucoup étudiée en géométrie, mais difficile à résoudre numériquement. Dans un certain nombre de cas, cette équation se ramène à un problème de transport optimal.
Le transport optimal est un domaine très actif des mathématiques depuis les années 1990, et a été notamment au cœur des recherches de Cédric Villani et Alessio Figalli, des mathématiciens récompensés récemment par des médailles Fields.
Le transport optimal intervient en mathématiques fondamentales, mais est aussi utilisé pour formuler des problèmes venant de domaines très variés, de la chimie quantique au machine learning en passant aussi par l'optique.
De la théorie à la fabrication
Ces dernières années, des méthodes géométriques, appelées semi-discrètes, ont été utilisées pour discrétiser et résoudre numériquement des problèmes de transport optimal. Les premières mises en œuvre algorithmiques nécessitaient malheureusement un temps de calcul absolument prohibitif.
Dans un travail récent, qui sera publié prochainement dans le Journal of the European Mathematical Society, Jun Kitagawa (Université du Michigan), Quentin Mérigot (Université Paris-Sud) et Boris Thibert (Université Grenoble Alpes) ont développé et analysé mathématiquement un algorithme permettant en principe de résoudre des problèmes de transport optimal de très grandes tailles.
"
Le transport optimal est un problème qui nous intéresse depuis de nombreuses années, Quentin Mérigot et moi" raconte Boris Thibert "
Nous avons, avec Jun Kitagawa, proposé et analysé un algorithme qui permet de résoudre des problèmes de transport optimal dans un cadre général. Il s'agissait d'un travail théorique. Le travail avec Jocelyn Meyron a consisté à adapter cet algorithme pour construire des miroirs et des lentilles. Ce n’est pas si fréquent en mathématiques de produire des objets. Là, nous sommes allés jusqu’à la réalisation de lentilles et de miroirs."
Un algorithme générique
Et c’est l’aboutissement de ce travail qui fait l’objet de la publication des chercheurs dans la revue
Transactions on Graphics. Leur méthode permet de traiter plusieurs problèmes d'optique anidolique (sources ponctuelles ou parallèles, miroirs ou lentilles, composants convexes ou concaves, champs proches ou lointains) de manière unifiée, précise et complètement automatique. Les résultats ont été validés par des expériences numériques mais aussi par la création de prototypes physiques.
Un premier travail de reformulation mathématique et surtout de développement informatique conséquent permet de traiter des cibles lumineuses lointaines. L'article introduit également une approche itérative permettant de traiter des cibles plus réalistes, dites en champ proche, en partant de la solution du champ lointain.
Les chercheurs ont ainsi réussi à fabriquer une lentille qui, éclairée par une lumière parallèle uniforme comme celle du soleil, projette sur un mur l’image du caractère japonais Hikari, qui signifie lumière.

Figure 2 : Prototype physique. La lumière parallèle uniforme (comme les rayons du soleil) se projette sur un mur après réfraction à travers la lentille. La lentille a été conçue de telle manière à ce que l'image projetée forme le caractère japonais Hikari. (Photo issue de la l’article paru dans ACM Transactions on Graphics. Crédit : Mérigot / Meyron / Thibert)
Des composants optiques d’une précision étonnante
Le même algorithme permet en réalité de définir la forme d’une lentille ou d’un miroir capable de transformer une lumière parallèle et uniforme en n’importe quelle image.
"Au départ, en 2010, une entreprise nous avait contactés pour travailler sur l'automatisation de la construction des phares de voiture. Nous avons collaboré avec eux plusieurs années et travaillé en parallèle sur des problèmes de transport optimal et d'optique non-imageante. Nous sommes finalement arrivés à un résultat très précis, au-delà des attentes initiales" conclut Boris Thibert.
Notes
[*] Brevet n°1871709
Laboratoire Jean Kuntzmann : CNRS / Grenoble INP / Inria / Université Grenoble Alpes.
Laboratoire de mathématiques d'Orsay : Université Paris-Sud / CNRS.